Sine Law, Cosine Law, and Special Triangles: An Introduction Into Intermediate Concepts

Now that we have covered the fundamentals of trigonometry, let us advance to more involuted concepts. In this blog, we will be covering special triangles, sine law, and cosine law and their uses and affordances.

A special triangle is a triangle in trigonometry that always have the same ratio measures for side lengths and angles. A special triangle makes it exceptionally easy and simple to solve the triangle as minimal trigonometry is needed. In trigonometry, there are 2 special triangles. 1 of them is known as the "45, 45, 90 triangle" and the other is known as the "30, 60, 90 triangle". The numbers that these triangles are so famous for refer to their angles. A 30, 60, 90 triangle has a 30-degree angle, a 60-degree angle, and a right angle, as the name suggests. While a 45, 45, 90 triangle is a triangle with two 45-degree angles and a right angle. So, what is so special about these 2 triangles and what does that mean?

Let us go over the 30, 60, 90 triangle first. As previously mentioned, a 30, 60, 90 triangle is a triangle that has angles of 30, 60, and 90. But what does this mean? It means that in all 30, 60, and 90 triangles, the side opposite the 30-degree angle is half the length of the hypotenuse, and the length of the side opposite of the 60-degree angle is √3 times the length of the side opposite the 30-degree angle. Observe the reference below,

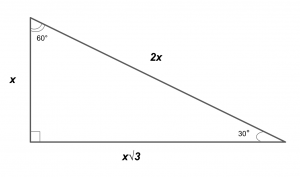
(Montgomery, 2020)

In the reference, we can see what I have mentioned above. This means essentially, that as long as you know the length of one or more of these sides, you can solve for the perimeter of the triangle without the Pythagorean Theorem or trigonometry.

Next, let's talk about the other special triangle, the 45, 45, and 90 triangle. Right off the bat, we have to acknowledge that a 45, 45, 90 triangle has 2 congruent sides, meaning that 2 of the side lengths have the same value. The next thing we need to know is that the hypotenuse is the length of the congruent side times the square root of 2. Observe the reference below,

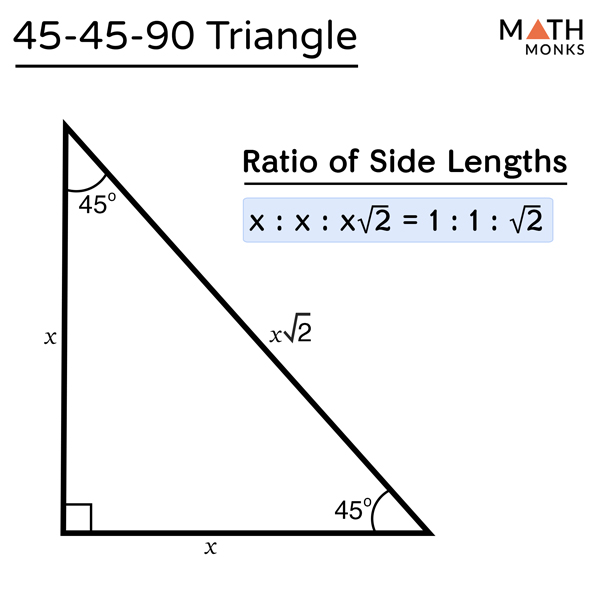
(Math Monks, 2023)

In the reference, we can see what I have mentioned above. 2 of the sides of the triangle are congruent, and the hypotenuse is the length of the congruent side times square root 2. Once again, the purpose of this is to help you solve a triangle's perimeter without using the Pythagorean Theorem or trigonometry when you know the side length for any one of the sides.

Now that we have covered the 2 special triangles within trigonometry, let's move on to something more advanced, sine and cosine law.

Remember how I previously mentioned that the trigonometry that we have explored so far only works on right triangles? Now we are going to explore laws that will work on any triangle that meets its specific requirements. Introducing: sine law and cosine law.

Firstly, let's start with sine law. In a triangle without a right angle, sine law is used when you either know two angles and any corresponding side, or two sides and a corresponding angle. What do I mean by this? Observe the reference below,

(underground mathematics, 2013)

As we can see, we have a triangle without a right angle. So, how can we fully solve the triangle? For that, we need to learn the equation of the sine law.

The equation for sine law is: sinA/a = sinB/b = sinC/c, with the capital letters referring to the angles, and the lowercase letters referring to the sides. Now that we know this, how can we utilize it to solve triangles such as the one above? Before we start solving, we first need to clarify the requirements for using sine law. As mentioned above, we must either know 2 side lengths with a corresponding angle, or 2 angles with a corresponding side. What does this mean?

Let's look at the reference above as an example. Say that two of your angles are defined, A and B, and they both have imaginary values. That means that the side that has a value must also be either a or b as the 2 have to correlate. If the side with value is c, sine law cannot be used in this case.

The same is true for both sides. Say that two of your side lengths are defined, a and b, and they both have imaginary values. This means that the angle which has a value must also be either A or B as the 2 have to correlate. If in this case, the angle that has value is C, sine law cannot be used.

Now that we have established some parameters, let's explore utilizing this law to solve a triangle. Observe the reference below,

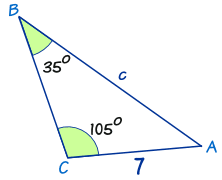
(Math is Fun, 2017)

In the reference, we can observe that we have the values of 2 angles as well as the value of 1 corresponding side. Now, how do we use this information and sine law to solve this triangle? The solution is surprisingly simple. All we have to do is to substitute each of the respective values into sine law's equation. Observe below,

sinA/a = SinB/b = SinC/c

Since we know the values of angles B and C and the value of the side length b, we can plug that into our equation.

sin35/7 = sin105/c

Since we do not know the values for either the angle or the side length of A, we can remove it from the equation for now.

Afterward, all we have to do is to solve for the undefined variable, c. To do this, we need to isolate c.

(sin35/7)(c) = sin105

c = sin105 / sin35/7

c ≈ 12

Now that we have both the b and c values, we are only 1 side away from completing the perimeter of the triangle. However, we do not have the requirements to solve the last side, so what do we do? Remember that in any triangle, the interior angles always add up to a sum of 180°. Since we already have 2 of the interior angles, we can use simple subtraction to find the value of the last angle.

180° = x + 105° + 35°

x = 40°

Using this knowledge, we now have the necessary components to solve this side. Let's start by writing an equation. Since we know all the values of the triangle except for side a, we can use any of the 3 angles/sides as long as one of them is a. In this example, we are going to be using b.

sin40/a = sin35/7

sin40 = (sin35/7)(a)

a = sin40 / sin35/7

a ≈ 8

And just like that, we have successfully solved an entire triangle using sine law. However, what happens when a triangle without a right angle appears but also the base triangle does not match any of the requirements needed to use sine law? Introducing cosine law, another law that helps solve a triangle without a right angle and with its own set of requirements.

Cosine law is used in a triangle without a right angle, and when you either know the side lengths of all 3 sides of the triangle or when you know 2 sides and a contained angle.

The formulas for cosine law are a^2 = b^2 + c^2 - 2bc cosa, b^2 = a^2 + c^2 -2ac cosb , and c^2 = a^2 + b^2 - 2ab cosc. The formula which you will use when solving depends on which side or angle you want to solve for. For example, if we were solving for b, using b^2 = a^2 + c^2 -2ac cosb is the most logical option. Observe the reference below,

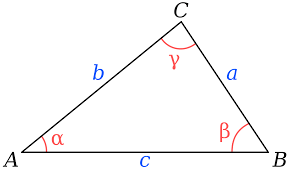
(Wikipedia Commons, 2023)

As we can see, we have a triangle without a right angle. So, how can we fully solve this triangle using cosine law?

First, let us examine a triangle where cosine law is possible. Observe below,

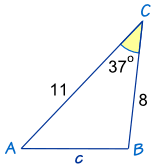
(Math is Fun, 2017b)

Let us start off by writing our equation.

c^2 = a^2 + b^2 - 2ab cosc

(A variation to our cosine law because we are trying to find the value for c)

Next, let's plug in our known values.

c^2 = 11^2 + 8^2 - (2(11)(8))((cos(37)

Now, we can begin to solve.

c^2 = 121 + 64 - (176)(0.8)

c^2 = 185 - 141

c = √44

c ≈ 6.6

Just like that, we have the values of all 3 sides. But how do we find the remaining angles to complete the rest of the triangle? By using cosine law.

Let's solve for the angle of B first. The first step is to write our equation.

b^2 = a^2 + c^2 - 2ac cosb

Then, we plug in all our known values.

8^2 = 11^2 + 6.6^2 - 2(11)(6.6) cosb

Now we can solve.

64 = 121 + 44 - (154)(cosb)

64 = 165 - (154)(cosb)

64/154 = 165/154 - cosb

cosb = 165/154 - 64/154

b = cos^-1 (165/154 - 64/154)

b = cos^-1 (0.66)

b = 49°

Now that we have 2/3 angles, and we know that in an angle there is always 180 degrees, we can do simple arithmetic to solve this triangle fully and to complete all the angles.

180 = x + 49 + 37

x = 94

a = 94°

And just like that, we have solved all of the unknowns in the triangle.

Overall, sine law, cosine law, and special triangles will be crucial in future mathematics and pertinent to your success in the field. Mastering these concepts will prove to be extremely beneficial when you are solving problems such as the ones presented in this blog.

Math is Fun. (2017a). The Law of Sines. Mathsisfun.com. https://www.mathsisfun.com/algebra/trig-sine-law.html Math is Fun. (2017b). Triangle. In Math is Fun. https://www.mathsisfun.com/algebra/trig-cosine-law.html Math Monks. (2023). 45-45-90 Triangle – Definition, Formula, Examples. Math Monks. https://mathmonks.com/triangle/45-45-90-triangle Montgomery, C. (2020, January 23). The Easy Guide to the 30-60-90 Triangle. Blog.prepscholar.com. https://blog.prepscholar.com/30-60-90-triangle-ratio-formula underground mathematics. (2013). Sine rule | Glossary | Underground Mathematics. Undergroundmathematics.org. https://undergroundmathematics.org/glossary/sine-rule Wikipedia Commons. (2023). A triangle. In Wikipedia. https://en.wikipedia.org/wiki/Law_of_cosines